前回までで、DirectXを使って3D描画の最小要素となるポリゴン(三角形1つ)の描画ができました。
ここからは、ポリゴン(頂点)を自由に移動・回転・サイズに変換できるように、ポリゴンの座標変換をできるようにしていきます。
今回はまず、頂点座標変換を効率的に行えるようにシェーダーで座標変換をするための基礎フローを実装していきます。
前回の記事:【3Dゲーム開発 – 12】ポリゴンの表示
3Dゲーム開発記事のまとめ:「3Dゲーム開発」
シェーダーに変換用の変数を渡す
座標変換自体は、行列の計算に慣れさえすれば難しいものではありません。
頂点の座標変換計算は、シェーダーではなくcppプログラム上でも出来はしますが、頂点の数は最終的なゲームでは膨大な数となるので、並列処理が得意なGPU側(シェーダー)で計算するのが基本です。
ということでやることは、頂点シェーダーに変換行列を伝えて、シェーダーで頂点座標を変換して描画していく、となります。
そのために必要な手順を以下で見ていきます。
定数バッファ用の構造体用意
変換行列はGPU側で参照できる「定数バッファ」に設定します。
定数バッファは、頂点バッファなどで作成したのと同様、CreateBufferメソッドで作成するGPU側参照できるリソースとなります。
定数バッファに渡すデータ内容は、構造体を定義して、そのサイズ・内容でバッファーへコピーするのが基本です。
ということでまずは、渡したいデータをもたせられる構造体を用意しましょう。
今回は以下のように変換行列1つのみをもつ構造体CbTransformを用意します。
また、定数バッファ(ID3D11Buffer)とセットで使うのでそのセットの構造体も用意しました。
struct CbTransform
{
XMFLOAT4X4 Transform;
};
struct CbTransformSet
{
CbTransform Data;
ID3D11Buffer* pBuffer = nullptr;
};
用意した構造体で、頂点バッファのときにも使ったCreateBufferメソッドで定数バッファを用意します。
bool RenderParam::initConstantBuffer(Renderer& renderer)
{
// 定数バッファの定義
D3D11_BUFFER_DESC cBufferDesc;
cBufferDesc.Usage = D3D11_USAGE_DYNAMIC;
cBufferDesc.BindFlags = D3D11_BIND_CONSTANT_BUFFER;
cBufferDesc.CPUAccessFlags = D3D11_CPU_ACCESS_WRITE;
cBufferDesc.MiscFlags = 0;
cBufferDesc.StructureByteStride = 0;
// 定数バッファ①の作成
cBufferDesc.ByteWidth = sizeof(CbTransform); // バッファ・サイズ
auto hr = renderer.GetDevice()->CreateBuffer(&cBufferDesc, nullptr, &CbTransformSet.pBuffer);
if (FAILED(hr)) {
return false;
}
return true;
}
定数バッファ用の構造体の実体は、今後描画向けのデータが増えることを見越して、RenderParamという構造体を新たに定義してそこに保持。
RendererがRenderParamを保持、という形で1段ラップして整理する形としています。
struct RenderParam
{
CbTransformSet CbTransformSet;
bool Initialize(Renderer& renderer);
void Terminate(Renderer& renderer);
private:
bool initConstantBuffer(Renderer& renderer);
};
bool RenderParam::Initialize(Renderer& renderer)
{
auto result = initConstantBuffer(renderer);
if (result == false) return false;
return true;
}
void RenderParam::Terminate(Renderer& renderer)
{
DX_SAFE_RELEASE(CbTransformSet.pBuffer);
}
2D変換行列の計算
では、座標変換を行列計算で実装してみましょう。
今回は見た目もコードもわかりやすい平行移動のみを行います。
DirectXMathを使って平行移動変換をするのが、以下のコードとなります。
auto mtx = XMMatrixTranslation(0.5f, 0.5f, 0);
XMStoreFloat4x4(&cb.Data.Transform, XMMatrixTranspose(mtx));
XMMatrixTranslationメソッドがその名の通り、移動処理を行う行列を取得できるメソッドです。
XMMatrixTranslation(0.5f, 0.5f, 0);これで、x方向0.5、y方向0.5の移動変換をしてくれる行列、ができたということです。簡単ですね。
転置行列計算で列優先配置に変換
次が座標変換の本質には無関係で、面倒なポイントなのですが、シェーダーで参照するの行列は「行列の転置」をして設定する必要があります。
これは行列には、「行優先配置」と「列優先配置」という、メモリ上の行列のデータの配置方法には2種類あり、そのどちらの形式になっているかが関係しています。
今回シェーダーコンパイル(D3DCompileFromFile)では、「列優先配置」の解釈がデフォルトの設定となっており、そのままデフォルト設定でコンパイルしています。
しかし、DirectXMathの行列(XMMATRIX構造体)では「行優先配置」であるため、行優先→列優先への変換が必要になります。これを行うのが「転置行列変換」です。
XMMatrixTranspose(mtx)がmtxの転置行列を計算するメソッドです。
XMStoreFloat4x4は、XMMATRIXをXMFLOAT4X4に格納するメソッドで、シェーダーなどに渡す行列は、XMFLOAT4X4構造体として渡すので、これで格納します。
参考:シェーダーコンパイルで行優先でコンパイルする
ちなみに、シェーダーコンパイルで行優先配置としてコンパイルも一応可能です。
D3DCompileFromFileにわたすFlagsにD3DCOMPILE_PACK_MATRIX_ROW_MAJORを設定します。
こうすることで、転置行列変換も不要にできます。ただ↓のドキュメントにも書いてありますが、列優先のほうがVectorとの乗算時などの計算効率がよいため、基本的に列優先で利用します。
定数バッファに変換行列を書き込み
定数バッファを使う用意ができたので、定数バッファに変換行列をセットしましょう。
定数バッファへの書き込みは、Mapメソッドでまず作成した定数バッファを書き込み可能とした上で、実際のデータ書き込み先となるサブリソースポインタを取得します(サブリソースについては、前回の記事参照)。
取得したサブリソースにCopyMemoryでデータをコピー、Unmapで書き込みを終了します。
このMapからUnmapまでの間は、GPUがリソースにアクセスできなくなり(ロックされている)、GPU側処理が進まなくなり、安全にデータ設定ができる、となります。
設定した定数バッファは、使うシェーダーにセットしてあげる必要があるので、今回はVertexShader用の変数なので、VSSetConstantBuffers(0, 1, &cb.pBuffer)でセットして準備完了です。これは、Slot0に、1つのバッファをセットするという呼び出しとなります。
以上を行ったコードが以下となります。
void Triangle::setupTransform(Renderer& renderer)
{
auto& cb = renderer.GetRenderParam().CbTransformSet;
auto mtx = DirectX::XMMatrixTranslation(0.5f, 0.5f, 0);
DirectX::XMStoreFloat4x4(&cb.Data.Transform, XMMatrixTranspose(mtx));
D3D11_MAPPED_SUBRESOURCE mappedResource;
// CBufferにひもづくハードウェアリソースマップ取得(ロックして取得)
auto pDeviceContext = renderer.GetDeviceContext();
HRESULT hr = pDeviceContext->Map(
cb.pBuffer,
0,
D3D11_MAP_WRITE_DISCARD,
0,
&mappedResource);
if (FAILED(hr)) {
//DXTRACE_ERR(L"DrawSceneGraph failed", hr);
return;
}
CopyMemory(mappedResource.pData, &cb.Data, sizeof(cb.Data));
// マップ解除
pDeviceContext->Unmap(cb.pBuffer, 0);
pDeviceContext->VSSetConstantBuffers(0, 1, &cb.pBuffer);
}
シェーダーで行列計算
これで、定数バッファにいれた変換行列を頂点シェーダーから参照可能となりました。
早速シェーダーで使ってみましょう。
上述のVSSetConstantBuffersでSlot0にセットする、という呼び出しをしたので、Slot0を参照して渡されるはずの定数バッファ宣言をすれば、利用可能です。
以下の通りです。
cbuffer cbTransform : register(b0) { // 常にスロット「0」を使う
matrix Transform;
};
float4 main( float4 pos : POSITION ) : SV_POSITION
{
return mul(pos, Transform);
}
mulは、シェーダー内の行列の乗算を行うメソッドです。
このコードで、pos(頂点座標)がTransformの座標変換行列が適用された座標へ座標変換されます。
結果
以上のコードを実行すると以下の結果となります。
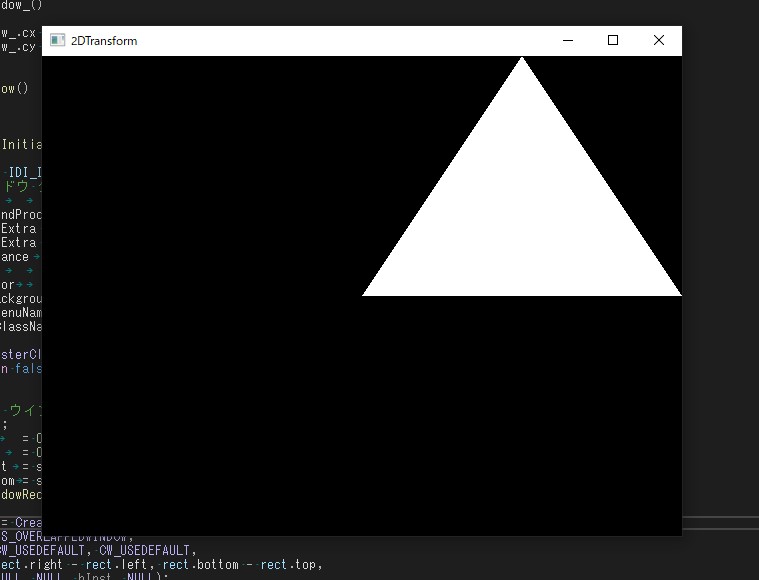
例として一番右の頂点でゆうと、(0.5f, -0.5f, 0.f)が、平行移動されて(1.0f, 0.f, 0.f)となっているのがわかります。


コメント
[…] 前回の記事:【3Dゲーム開発 – 13】ポリゴンの座標変換① : シェーダーで座標変換 […]