前回までで、DirectXMathを使って行列の用意、シェーダーで座標変換、ができました。
今回は、「移動」「回転」「スケール」それぞれの2D変換について詳しく見ていきましょう。
また、座標変換は、単体で終わるものではなく、移動・回転・スケールを組み合わせて使うのが通常。組み合わせた結果も見ていきましょう。

【3Dゲーム開発#04】ポリゴンの座標変換① : シェーダーで座標変換
前回までで、DirectXを使って3D描画の最小要素となるポリゴン(三角形1つ)の描画ができました。ここからは、ポリゴン(頂点)を自由に移動・回転・サイズに変換できるように、ポリゴンの座標変換をできるようにしていきます。今回はまず、頂点座標...
前回の記事:【3Dゲーム開発 – 13】ポリゴンの座標変換① : シェーダーで座標変換
3Dゲーム開発記事のまとめ:「3Dゲーム開発」
まずは正三角形にしよう
色々な2D変換をしていくにあたって、座標変換結果をわかりやすくするために、これまで描画してきた三角形を正三角形にしましょう。
(これまで描画してきた三角形も正三角形っぽくも見えますが、正三角形ではありません。)
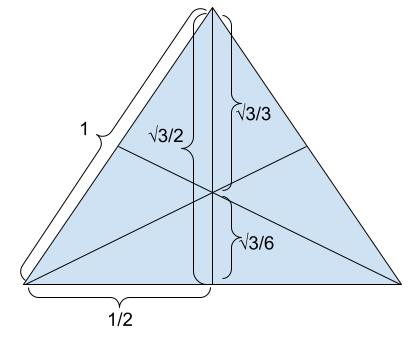
まず正三角形の辺の長さの比は以下の図のようになります。
これは、中学数学の知識
- 30°、60°、90°で構成される直角三角形の辺の比は、2:1:√3 となる
- 各頂点とその対辺の中点を結ぶ線は1点で交わりこの点を重心といい、その点は各中線を2:1に内分する
あたりを理解しているとなんとなくわかると思います。このへんの数学が苦手な場合、参考程度に読み流してください。
この図から、重心を原点とした場合の正三角形の座標は、以下のようになり、Triangleの初期座標として設定します。
// √3
auto sqrt3 = sqrtf(3);
Vertices[0] = { 0.f, sqrt3 / 3.f, 0.f };
Vertices[1] = { 0.5f, -sqrt3 / 6.f, 0.f };
Vertices[2] = { -0.5f, -sqrt3 / 6.f, 0.f };
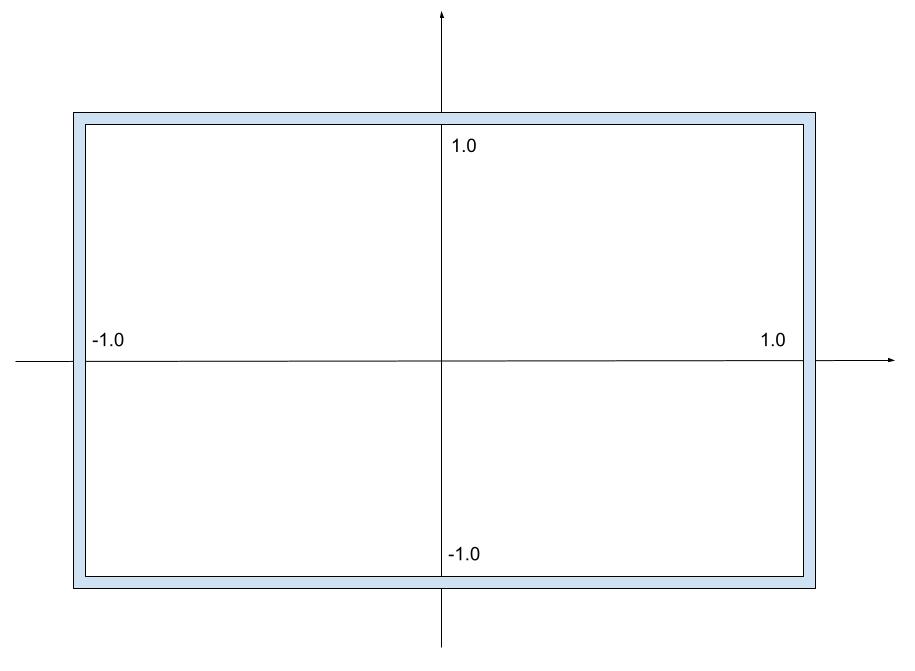
また座標は、スクリーン上の座標を直接指定して描画しており、以下のような座標系となっています。
これは、画面がどんな大きさだろうと、画面の端が(-1,-1)~(1,1)に収まるような座標系ということです(これをスクリーン座標系といいます)。
座標系はX軸、Y軸とも-1~1の値域となるものの、実際のスクリーンサイズは現状は640 x 480ということで、X軸とY軸で画面における1単位の長さが異なっています(アスペクト比が違う)。
これを正しい座標の比にするには
- 座標にスクリーンの座標比を考慮した補正をかける(アスペクト比の逆がけをする) or
- スクリーン座標比を1:1にする(スクリーンを正方形にする)
といった手段がとれます。
本来はスクリーンサイズは自由にしたいので、1の手段をとるべきですが、今回は手っ取り早い2の手段でいきましょう(1の手段は3D変換になったら否が応でもやることになります)。
ということで、Windowクラスのスクリーンサイズを480 x 480の正方形にしておきます。
sizeWindow_.cx = 480;
sizeWindow_.cy = 480;
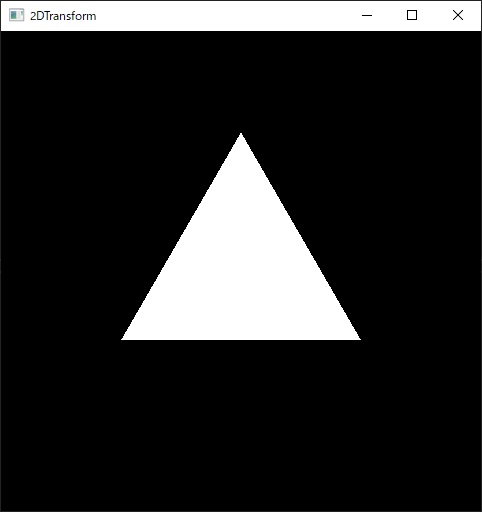
これで準備が整い以下のように正三角形が表示されます。
2次元での平行移動 (2D Translation)
2次元座標変換は、通常XZ平面上での2次元平面を指します。
ですので、平行移動は、X成分、Y成分の移動をしていきます(Zは0のままいじらない)。
平行移動のための行列は、DirectXMathのAPIを使って以下で求まります。
auto mtx = XMMatrixTranslation(translateX_, translateY_, 0);
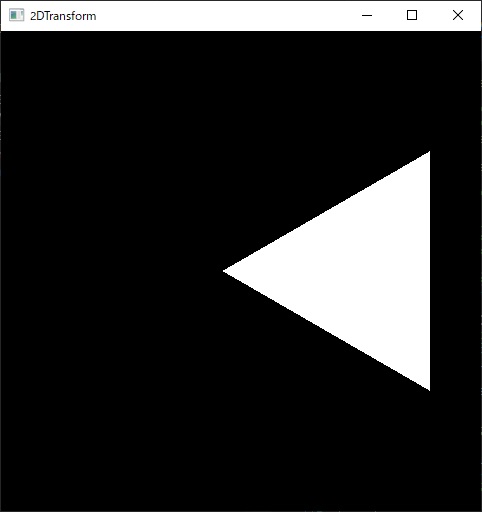
前回やったとおり、この行列を定数バッファにセットして利用すれば以下のように平行移動します。
translateX_、translateY_を毎フレーム少しずつ[-1,1]の範囲で変化するようにして動かしています。
2次元での回転 (2D Rotation)
2次元での回転も同様にXY平面上での回転を考えます。
となると、XY平面と直行する軸「Z軸」による回転を行えばXY平面で回転します。
Z軸で回転させる行列は、DirectXMathのAPIを使って以下で求まります。
auto mtx = XMMatrixRotationZ(angle_);
回転させると以下のようになります。
angle_を、毎フレーム少しずつ増加させて変化するようにしています。
2次元での拡大縮小 (2D Scale)
2次元での拡大・縮小も同様にXY平面上で考えます。
XZ成分でスケールする行列は、DirectXMathのAPIを使って以下で求まります。
auto mtx = XMMatrixScaling(scale_, scale_, 1.f);
スケールさせると以下のようになります。
scale_を毎フレーム少しずつ[0.5,2.0]の範囲で変化するようにしています。
各種座標変換を組み合わせる
以上で各2次元座標変換ができました。
しかし、実用上は各変換を組み合わせて使うことが多くなります。
その際に重要になるのが「変換を適用する順番」です。
適用順による違いは実際に見てみるのが一番です、以下でいくつかの組み合わせを見ていきましょう。
回転 x 移動
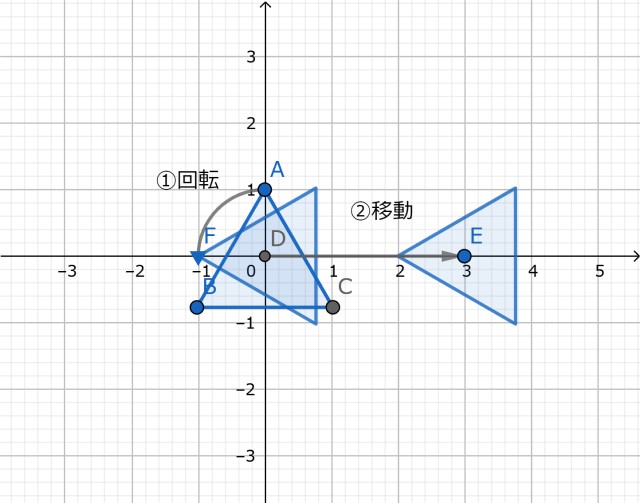
回転してから移動
「回転してから移動」の変換として以下の順に処理します。
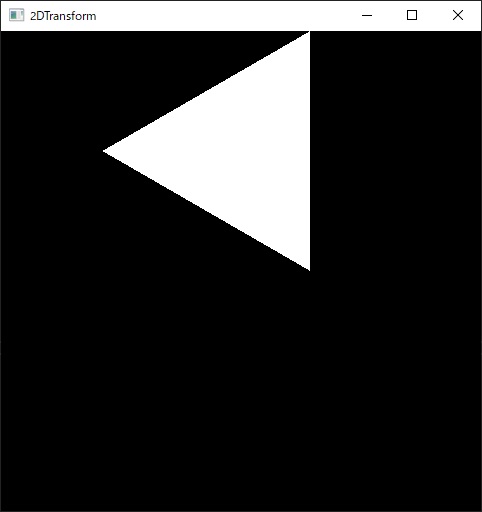
その結果が以下( 変換前(左) → 変換後(右) )です。
これは、変換過程を図示すると以下の通りです(座標は見やすくするため一部変更)。
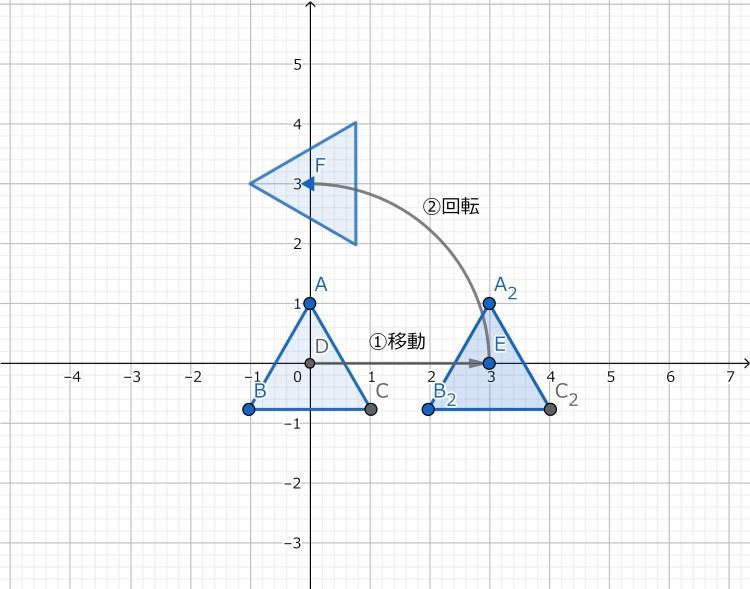
移動してから回転
「移動してから回転」の変換として以下の順に処理します。上の順番を逆に下だけです。
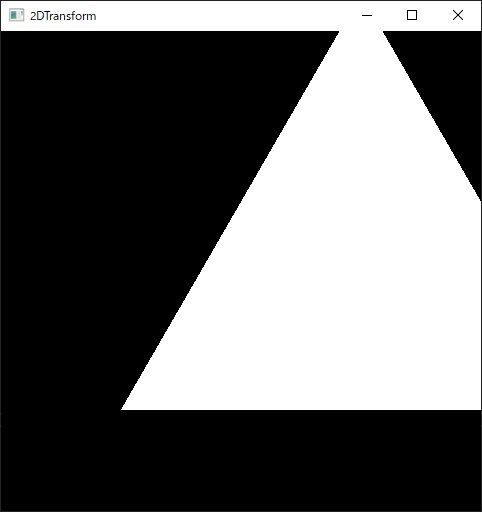
その結果が以下( 変換前(左) → 変換後(右) )です。逆にしただけで全く結果が異なることがわかります。
これは、変換過程を図示すると以下のようになるためです。
三角形という物体が、移動量分の半径をもつ円を回るような変換がされます。
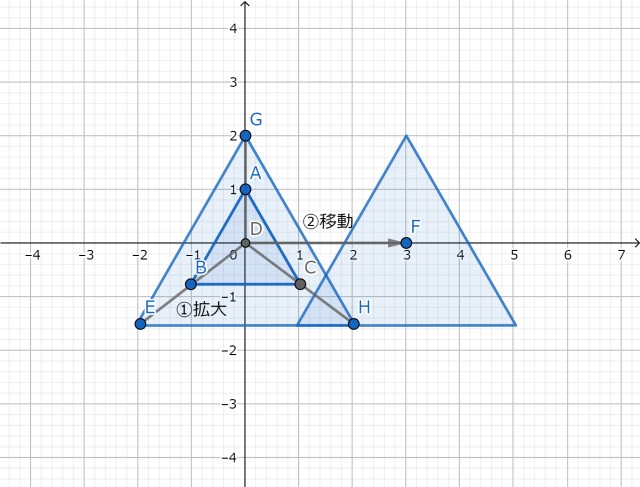
スケール x 移動
スケールしてから移動
「スケール(拡大)してから移動」の変換として以下の順に処理します。
その結果が以下( 変換前(左) → 変換後(右) )です。
これは、変換過程を図示すると以下の通りとなります。
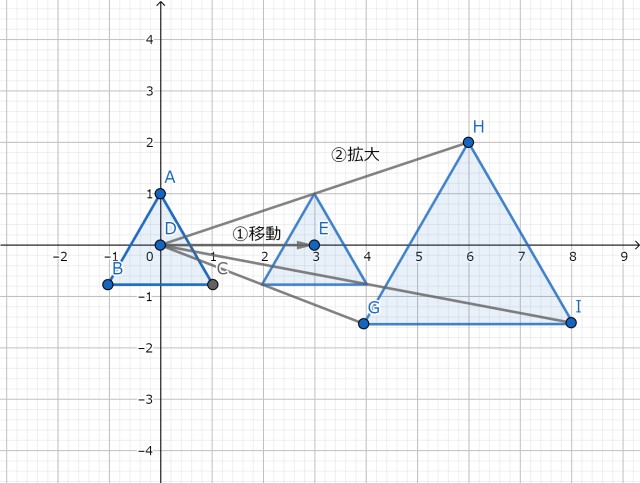
移動してからスケール
「移動してから回転」の変換として以下の順に処理します。上の順番を逆に下だけです。
その結果が以下( 変換前(左) → 変換後(右) )です。
変換順が逆の場合と、三角形の位置が変わっていることがわかります。
これは、変換過程を図示すると以下の通りとなるためです。
三角形自体の大きさも、移動量にも、スケールが効くような結果となります。
座標変換の考え方
座標変換の順番による違いを見てみて、納得のものや、意外とわかりにくい結果になるものもあったりしたかと思います。
考え方のポイントとしては以下のような点です。
- 座標変換は原点を中心に行われることを意識
- 点に対する変換を考える
まず、基本ですが、各座標変換の基準はあくまで(0,0)、つまり原点です。
もちろんゲーム処理では、原点以外を中心に座標変換したい、ということはありますが、それも、座標変換をどういった順番で組み立てて行えば求める結果になるか、というだけで、あくまで単体としての座標変換は原点中心です。
それから、三角形で考えるとどうしても、三角形の中心を基準に考えがちになることがあります。
(例えば、移動→スケールの場合に、スケールを移動先の座標を中心に拡大するイメージになる)
ここで、あくまで点(例えば三角形の1頂点のみ)のことを考えると、三角形の中心座標、みたいな概念がなくなるので、自然と原点中心で考えられます。
よく使う変換順序とは(ゲーム開発)
組み合わせ・順番で様々な変換ができることがわかったと思います。
ただゲーム開発でよく使う変換はだいたい決まっていて、
まずは、スケール x 回転 x 移動 が基本です。
例えばキャラクターAが、2倍の大きさで、90度方向を向いていて、X方向に1mの位置、とする場合、などがゲームではよくつかう座標変換の例です。
この場合、まずキャラの大きさ・向きを整えてから、移動させてあげる、というのがやりたいこととなるからです。
ただ、これしか使わない、ということでもないです。
例えば、惑星の動きのような、何かを基準に一定距離の位置で回転させるような場合、移動先からさらに回転といった変換となります。
ソースコード
本記事にソースコードは以下となります。また、GitHub/prog-logの方にも公開されています。

GameDev/03-2DTransform/RenderParam.cpp at master · prog-log/GameDev
Contribute to prog-log/GameDev development by creating an account on GitHub.
#include "Renderer.h"
#include
#pragma comment(lib, "d3dcompiler.lib")
Renderer::Renderer()
{
pFeatureLevels_[0] = D3D_FEATURE_LEVEL_11_1;
pFeatureLevels_[1] = D3D_FEATURE_LEVEL_11_0;
pFeatureLevels_[2] = D3D_FEATURE_LEVEL_10_1;
pFeatureLevels_[3] = D3D_FEATURE_LEVEL_10_0;
}
Renderer::~Renderer()
{
}
bool Renderer::Initialize(HWND hWindow)
{
// Windowに合わせてスクリーンサイズ初期化
RECT rc;
GetClientRect(hWindow, &rc);
screenWidth_ = rc.right - rc.left;
screenHeight_ = rc.bottom - rc.top;
initDeviceAndSwapChain(hWindow);
initBackBuffer();
CompileShader(L"VertexShader.hlsl", L"PixelShader.hlsl", defaultShader_);
renderParam_.Initialize(*this);
sampleTriangle_.CreateVertexBuffer(*this);
return true;
}
void Renderer::Terminate()
{
sampleTriangle_.DestroyVertexBuffer();
renderParam_.Terminate(*this);
// デバイス・ステートのクリア
if(pImmediateContext_)
pImmediateContext_->ClearState();
// スワップ チェインをウインドウ モードにする
if (pSwapChain_)
pSwapChain_->SetFullscreenState(FALSE, nullptr);
DX_SAFE_RELEASE(pRenderTargetView_);
DX_SAFE_RELEASE(pSwapChain_);
DX_SAFE_RELEASE(pImmediateContext_);
DX_SAFE_RELEASE(pD3DDevice_);
defaultShader_.Terminate();
}
void Renderer::Draw()
{
if (!pImmediateContext_ || !pRenderTargetView_) return;
pImmediateContext_->OMSetRenderTargets(1, &pRenderTargetView_, nullptr);
float color[] = { 0.f, 0.f, 0.f, 0.f };
pImmediateContext_->ClearRenderTargetView(pRenderTargetView_, color);
pImmediateContext_->IASetInputLayout(defaultShader_.pInputLayout);
pImmediateContext_->IASetPrimitiveTopology(D3D_PRIMITIVE_TOPOLOGY_TRIANGLELIST);
pImmediateContext_->VSSetShader(defaultShader_.pVertexShader, nullptr, 0);
pImmediateContext_->PSSetShader(defaultShader_.pPixelShader, nullptr, 0);
sampleTriangle_.Draw(*this);
}
void Renderer::Swap()
{
// バックバッファの表示(画面をすぐに更新)
HRESULT hr = pSwapChain_->Present(0, 0);
if (FAILED(hr)) {
//TRACE("Swap failed(%0x08x)\n", hr);
return;
}
}
bool Renderer::CompileShader(const WCHAR* vsPath, const WCHAR* psPath, Shader& outShader)
{
ID3DBlob* vsBlob = nullptr;
ID3DBlob* errBlob = nullptr;
auto pDevice = GetDevice();
// シェーダーコンパイル
auto hr = D3DCompileFromFile(
vsPath,
nullptr,
D3D_COMPILE_STANDARD_FILE_INCLUDE,
"main",
"vs_4_0",
D3DCOMPILE_DEBUG | D3DCOMPILE_SKIP_OPTIMIZATION,
0,
&vsBlob,
&errBlob
);
if (FAILED(hr)) return false;
// 頂点シェーダ作成(シェーダオブジェクト作成)
ID3D11VertexShader* pVertexShader = nullptr;
hr = pDevice->CreateVertexShader(
vsBlob->GetBufferPointer(),
vsBlob->GetBufferSize(),
nullptr,
&pVertexShader
);
if (FAILED(hr)) return false;
// 入力レイアウトオブジェクト作成
ID3D11InputLayout* pInputLayout = nullptr;
D3D11_INPUT_ELEMENT_DESC layout[] = {
{ "POSITION", 0, DXGI_FORMAT_R32G32B32_FLOAT, 0, 0, D3D11_INPUT_PER_VERTEX_DATA, 0 },
};
hr = pDevice->CreateInputLayout(
layout,
_countof(layout),
vsBlob->GetBufferPointer(),
vsBlob->GetBufferSize(),
&pInputLayout
);
if (FAILED(hr)) return false;
// ピクセルシェーダー作成
ID3DBlob* psBlob = nullptr;
hr = D3DCompileFromFile(
psPath,
nullptr,
D3D_COMPILE_STANDARD_FILE_INCLUDE,
"main",
"ps_4_0",
D3DCOMPILE_DEBUG | D3DCOMPILE_SKIP_OPTIMIZATION,
0,
&psBlob,
&errBlob
);
ID3D11PixelShader* pPixelShader = nullptr;
hr = pDevice->CreatePixelShader(
psBlob->GetBufferPointer(),
psBlob->GetBufferSize(),
nullptr,
&pPixelShader
);
if (FAILED(hr)) return false;
outShader.pVertexShader = pVertexShader;
outShader.pPixelShader = pPixelShader;
outShader.pInputLayout = pInputLayout;
return true;
}
bool Renderer::initDeviceAndSwapChain(HWND hWindow)
{
// デバイスとスワップ・チェイン作成
DXGI_SWAP_CHAIN_DESC sd;
ZeroMemory(&sd, sizeof(sd));
sd.BufferCount = backBufferNum_; // バックバッファの数
sd.BufferDesc.Width = screenWidth_; // バックバッファの幅
sd.BufferDesc.Height = screenHeight_; // バックバッファの高さ
sd.BufferDesc.Format = DXGI_FORMAT_R8G8B8A8_UNORM; // フォーマット
sd.BufferDesc.RefreshRate.Numerator = 60; // リフレッシュレート(分母)
sd.BufferDesc.RefreshRate.Denominator = 1; // リフレッシュレート(分子)
sd.BufferDesc.ScanlineOrdering = DXGI_MODE_SCANLINE_ORDER_PROGRESSIVE;
sd.BufferDesc.Scaling = DXGI_MODE_SCALING_CENTERED;
sd.BufferUsage = DXGI_USAGE_RENDER_TARGET_OUTPUT; // バックバッファの使用法
sd.OutputWindow = hWindow; // 関連付けるウィンドウ
sd.SampleDesc.Count = 1; // マルチサンプル(アンチエイリアス)の数
sd.SampleDesc.Quality = 0; // マルチサンプル(アンチエイリアス)のクオリティ
sd.Windowed = TRUE; // ウィンドウモード(TRUEがウィンドウモード)
sd.Flags = DXGI_SWAP_CHAIN_FLAG_ALLOW_MODE_SWITCH; // モード自動切り替え
#if defined(DEBUG) || defined(_DEBUG)
UINT createDeviceFlags = D3D11_CREATE_DEVICE_DEBUG;
#else
UINT createDeviceFlags = 0;
#endif
const D3D_DRIVER_TYPE DriverTypes[] = {
D3D_DRIVER_TYPE_HARDWARE,
D3D_DRIVER_TYPE_WARP,
D3D_DRIVER_TYPE_REFERENCE,
};
HRESULT hr;
for (auto type : DriverTypes) {
// ハードウェアデバイスを作成
hr = D3D11CreateDeviceAndSwapChain(
nullptr, type, nullptr, createDeviceFlags,
pFeatureLevels_, FEATURE_LEVELS_NUM, D3D11_SDK_VERSION, &sd,
&pSwapChain_, &pD3DDevice_, &featureLevelsSupported_, &pImmediateContext_);
if (SUCCEEDED(hr)) {
break;
}
}
if (FAILED(hr)) return false;
return true;
}
bool Renderer::initBackBuffer()
{
HRESULT hr;
// スワップ・チェインから最初のバック・バッファを取得する
ID3D11Texture2D *pBackBuffer; // バッファのアクセスに使うインターフェイス
hr = pSwapChain_->GetBuffer(
0, // バック・バッファの番号
__uuidof(ID3D11Texture2D), // バッファにアクセスするインターフェイス
(LPVOID*)&pBackBuffer); // バッファを受け取る変数
if (FAILED(hr)) {
//TRACE("InitBackBuffer g_pSwapChain->GetBuffer(%0x08x)\n", hr); // 失敗
return false;
}
// バック・バッファの情報
D3D11_TEXTURE2D_DESC descBackBuffer;
pBackBuffer->GetDesc(&descBackBuffer);
// バック・バッファの描画ターゲット・ビューを作る
hr = pD3DDevice_->CreateRenderTargetView(
pBackBuffer, // ビューでアクセスするリソース
nullptr, // 描画ターゲット・ビューの定義
&pRenderTargetView_); // 描画ターゲット・ビューを受け取る変数
DX_SAFE_RELEASE(pBackBuffer); // 以降、バック・バッファは直接使わないので解放
if (FAILED(hr)) {
//TRACE("InitBackBuffer g_pD3DDevice->CreateRenderTargetView(%0x08x)\n", hr); // 失敗
return false;
}
// ビューポートの設定
viewPort_[0].TopLeftX = 0.0f; // ビューポート領域の左上X座標。
viewPort_[0].TopLeftY = 0.0f; // ビューポート領域の左上Y座標。
viewPort_[0].Width = static_cast(screenWidth_); // ビューポート領域の幅
viewPort_[0].Height = static_cast(screenHeight_); // ビューポート領域の高さ
viewPort_[0].MinDepth = 0.0f; // ビューポート領域の深度値の最小値
viewPort_[0].MaxDepth = 1.0f; // ビューポート領域の深度値の最大値
pImmediateContext_->RSSetViewports(1, &viewPort_[0]);
return true;
}
#include
#include "Application.h"
int WINAPI WinMain( HINSTANCE hInst, HINSTANCE, LPSTR, int)
{
Application* application = new Application();
application->Initialize(hInst);
application->Loop();
application->Terminate();
delete(application);
return 0;
}










コメント
[…] […]
[…] […]